Gereç ve Yöntem: Açık kaynak kodlu bir R paketi olan Shiny, önerilen web yazılımını geliştirmek için kullanıldı. Geliştirilen yazılımda tek değişkenli normal dağılıma uygunluk için Shapiro-Wilk ve Anderson-Darling testleri, çok değişkenli normal dağılıma uygunluk için ise Mardia’nın çarpıklık-basıklık, Henze-Zirkler ve Doornik-Hansen testleri kullanıldı. Normal dağılıma uygunluk için verilen çıktılarda test istatistiklerine ilaveten grafiksel yöntemler de sunulmuştur. Örnek uygulama olarak simulasyon ile türetilen iki değişkenli, her bir değişkenin standart normal dağılıma sahip olduğu ve 1000 gözlemli veri seti için normal dağılıma uygunluk test edilerek bulgular değerlendirilmiştir.

Bulgular: Türetilen veri setinde her bir değişken Anderson-Darling ve Shapiro-Wilk testlerine göre normal dağılmıştır (sırasıyla x1 ve x2 değişkenleri için p =0.91 ve p =0.707; p =0.756 ve p =0.573). Ayrıca türetilen veri seti Mardia’nın çarpıklık-basıklık, Henze-Zirkler ve Doornik-Hansen testlerine göre iki değişkenli normal dağılım göstermiştir (respectively p =0.826, p =0.831 and p =0.868).

Sonuç: Geliştirilen yazılım tek değişkenli ve çok değişkenli normal dağılıma uygunluk analizlerini kolayca yapabilen ve kullanıcıların yapacakları çalışmalarında daha doğru sonuçlar elde etmesini sağlayan yeni kullanıcı dostu bir web tabanlı yazılımdır. İlerleyen çalışmalarda, en iyi yönteme karar vermede kullanılan ölçütlerden Tip I ve Tip II hata türlerinin yazılıma eklenmesi planlanmaktadır.

Güçlü olarak kabul edilen çoğu istatistiksel testler veri setinin normal dağılıma uygun olması varsayımı altında çalışmaktadır. Bu nedenle istatistiksel analizlere başlanmadan veri setinin normal dağılıp dağılmadığı araştırılmalıdır. Bu nedenle normal dağılım istatistik alanında en çok üzerinde durulan konulardan biri oluştur. De Moivre tarafından 1733 yılında temelleri binom dağılımın limit şekli olarak atılmış olsa da 1800’lü yılların başlarında Laplace ve Gauss tarafından geliştirilerek son halini almıştır. Genel olarak normal dağılım, veri setinde yer alan bağımlı değişken sayısına göre ‘tek değişkenli normal dağılım’ ve ‘çok değişkenli normal dağılım’ olmak üzere 2 kategoride sınıflandırılmaktadır. Tek değişkenli normallik varsayımında örneklemde yer alan her bir sürekli değişkene ait ölçümlerin normal dağılımdan gelmesi varsayımı vardır ^2,3. Sürekli tek bir değişkenin normalliği tanımlayıcı, grafiksel ve istatistiksel yöntemlerle incelenebilir ⁴.

Bağımlı değişkenlerin sürekli değişken olduğu tek ve çok değişkenli parametrik testler tek değişkenli normallik varsayımına, çok değişkenli parametrik testler ise ayrıca çok değişkenli normallik varsayımlarına dayandırılır ^5,6. Birden çok değişkenin aynı andan normallik koşulunu sağlaması anlamına gelen çok değişkenli normal dağılım, örneklemdeki her bir değişkenin tek değişkenli normallik şartını sağlamasına ek olarak değişkenlerin tüm doğrusal kombinasyonlarının ve her türlü elde edilebilen ikili kombinasyonlarının da her bir grup ve alt grup için normal oluğunu varsaymaktadır ⁶. Tek değişkenli normallik varsayımının incelenmesinde olduğu gibi çok değişkenli normal dağılımın varlığının araştırılması için de betimsel, grafiksel ve istatistiksel metotlar bulunmaktadır. Çok değişkenli normallik varsayımlarını incelemek için betimsel yöntem olarak çok değişkenli çarpıklık ve basıklık katsayıları kullanılabilmektedir ⁷. Grafiksel yöntem olarak çoklu saçılma grafiğinin yanı sıra marjinal grafikler, Kowalski’nin çizgi grafikleri çok değişkenli Q-Q grafikleri tercih edilebilir ⁵. Ayrıca tek değişkenli uyum iyiliği testlerinden olan Cramer-von Mises ⁸ testinden elde edilmiş Koziol’s testi ^9, Shapiro-Wilk elde edilmiş türetilmiş Mudholkar-Srivastava-Lin testi ^10, Anderson-Darling testinden elde edilmiş Paulson-Roohan-Sullo testi ^11, ki-kare testi ve Kolmogorov-Smirnov testinden elde edilmiş bazı testler kullanılabilmektedir ¹².

Araştırmalarda parametrik testler tercih edilmesine rağmen çok az sayıdaki çalışmalarda tek değişkenli ve bilhassa çok değişkenli normallik koşullarının gerçekleşip gerçekleşmeme durumunun kontrol edildiği sonucuna ulaşılmaktadır ¹³. Bu araştırma kapsamında çok değişkenli normal dağılıma uygunluğu kolay bir şekilde kontrol edecek ve kullanıcıların yapacakları çalışmalarında daha doğru sonuçlar elde etmesini sağlayacak yeni kullanıcı dostu bir web tabanlı yazılım geliştirmek amaçlanmıştır.

Normallik analizleri
Bu web tabanlı yazılım araştırıcıların sahip olduğu veri setlerini tek ve çok değişkenli normal dağılıma uygunluğunu test etmek amacıyla geliştirilmiştir. Geliştirilen yazılımda tek değişkenli normal dağılıma uygunluk Shapiro-Wilk ve Anderson-Darling testleri ile test edilirken, çok değişkenli normal dağılıma uygunluk ise Mardia’nın çarpıklıkbasıklık, Henze-Zirkler ve Door-nik-Hansen testleri ile test edilmektedir. Bu testler dışında yer alan ve normallik sınamasında kullanılabilen grafiksel metotlardan olan Q-Q, çekirdek yoğunluk kestirim ve 3-boyutlu yüzey grafikleri de araştırmacıların kullanımı amacıyla yazılımda yer almaktadır. Ayrıca geliştirilen yazılım ile veri seti yapısına bağlı olarak veride nitel değişken(ler)in varlığı durumunda alt grup analizlerinin yapılmasına olanak sağlanmıştır.

Shapiro-Wilk Testi
Normallik testlerinden olan Shapiro-Wilk testi ilk defa Samuel Shapiro ve Martin Wilk tarafından 1965 yılında yayınlanmıştır ¹⁴. Bu test için kurulacak sıfır hipotezi bir örneklemden elde edilen veri serisinin normal dağılım gösteren bir topluma ait olmasıdır. Yani 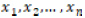serisinin normal dağılım gösteren bir topluma ait olmasıdır. Shapiro-Wilk test istatistiği olan W şu şekilde elde edilir: Küçükten büyüğe doğru sıralanmış 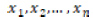için normal dağılım değerleri olan α_i değerleri şöyle bulunur.

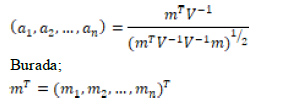
olup 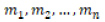standart normal dağılımdan örneklem olarak bulunmuş bağımsız ve aynı dağılımı gösteren rastgele değişkenlerin sıra istatistikleri değerlerine ait beklenen değerlerdir. V ise bu sıra istatistikleri için elde edilen kovaryans matrisidir. Son olarak W istatistiği ise

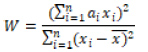
olarak elde edilir ¹⁴.

W test istatistiği 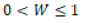aralığında değişim göstermektedir. W test istatistiğinin 1’e yakın değerler alması değişkenin normal dağılıma sahip olduğunu, 0’a yakın değerler alması ise değişkenin normal dağılıma sahip olmadığını gösterir ¹⁴.

Anderson-Darling Testi
Anderson-Darling testi deneysel dağılım fonksiyonu istatistiklerine dayandırılarak 1974 yılında Anderson ve Darling tarafından geliştirilen bir testtir. Bu testte uygulanacak verilerin ham veri olması gerekir. Anderson-Darling testi gözlenen birikimli dağılım fonksiyonunun beklenen birikimli dağılım fonksiyonuna uyumunu karşılaştırabilmek içn kullanılan bir testtir ¹⁴.

Anderson-Darling testi büyüklük sırası gösteren χ_i gözlemlerinin deneysel yığılımlı olasılık dağılımının yığılımlı standart normal dağılıma uygun olup olmadığını test eder. Bu işlem için her bir gözlemin standart dönüşümleri yapılarak Ζ_i gözlemleri elde edilir. Böylece elde edilen standart Ζ_i değerlerinin olasılıklarının standart normal dağılıma uygunluğu test edilir. Bu nedenle Anderson-Darling testinden bir Α² test istatistiği hesaplanarak verilerin normal dağılıma uygunluğu test edilir. Α² Anderson-Darling test istatistiği

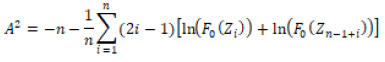
olarak elde edilir. Burada yer alan F₀(Ζ_i) değeri; standart normal dağılımın Ζ_i noktasındaki yığılımlı olasılık değerini, n ise örnek gözlem sayısını göstermektedir ¹⁴. Α² test istatistiği küçük örneklem genişliğine sahip veri setleri içn düzeltilerek kullanılır. Düzeltilmiş Α² test istatistiği ise

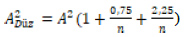
ile elde edilir ¹⁴.

Mardia’ nın çarpıklık-basıklık testi
Mardia tarafından önerilen ve çok değişkenli çarpıklık ve basıklık testleri, tek değişkenli çarpıklık ve basıklık ölçümlerini içeren t istatistiğinin gücünü genişletme çalışmaları ile 1970 yılında geliştirilmiştir. Ortalama değeri µ ve kovaryans matrisi µ olan p değişkenli bir evrende X için Mardia evrene ait çok değişkenli çarpıklık ve basıklık ölçümlerini aşağıdaki gibi vermiştir ^15,16.

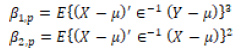Burada X ve Y bağımsız olarak özdeş olarak dağılır. Çok değişkenli çarpıklık ve basıklık katsayıları sırasıyla (Ŷ_1p) ve (Ŷ_2p) katsayılarına bağlı olarak hesaplanır. (χ₁, χ₂, ...χ_n) verisinin ortalama değeri ve kovaryans matrisi olan p değişkenli bir evrenden rastgele alınarak elde edilen bir örnek olduğu kabul edilirse, buna ait çok değişkenli çarpıklık ve basıklık katsayıları;

dir. Elde edilen katsayılara bağlı olarak çarpıklık ve basık-lık testi için sırasıyla elde edilecek test değerleri

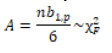
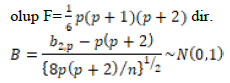
ile hesaplanır ¹⁶.

Henze-Zirkler
Henze-Zirkler testi Epps ve pulley tarafından 1983 yılında geliştirilen tek değişkenli normalliğin belirlenmesi için önerilen testin çok değişkenli normal dağılım durumu için genelleştirilmiş halidir. Ayrıca 1988 yılında Baringhaus ve Henze tarafından önerilen testin de genel halidir ¹⁷.

Çok değişkenli normal dağılımı belirlemek için kullanılan Henze-Zirkler test istatistiği düzleştirme parametresi olan β nın bir fonksiyonu olup

Doornik-Hansen
Doornik ve Hansen tarafından 1994 yılında geliştirilen bu test Bowman ve Shenton tarafından 1975 yılında önerilen çarpıklık ve basıklık katsayılarına bağlı geliştirilen tek değişkenli normallik testi test istatistiğinin çok değişkenli halidir. 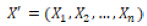bir veri kümesi, p boyutlu bir vektörde n gözlemli pxn boyutlu bir matris olduğunda örneklem ortalaması 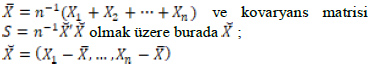dir. Standart sapmaların tersleriyle köşegen (diyagonal) matris;

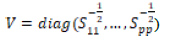
korelasyon matrisi C=VSV şeklinde oluşturulur. Verilerin dönüştürülmesi ile ilgili pxn boyutlu matris

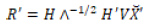
şeklinde tanımlanır.

Burada 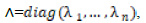köşegen (diyagonal) elemanlarda C’nin özdeğerli matrisidir. H’nin sütünları özvektörlerdir. Öyle ki 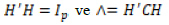dir. C ve V için popülasyon değerlerini kullanarak çok değişkenli normal dağılım, bağımsız standart normal dağılımlara dönüştürülebilir. Dönüştürülen gözlem değerlerinden tek değişkenli eğrilik ve diklik katsayıları hesaplanabilir.

Doornik-Hansen testi için test istatistiği,

Dosya yükleme
Bu web tabanlı uygulamanın ilk aşamasında, veri kümesini içeren dosya yüklenir. Veri analizinde farklı uzantılara sahip en yaygın kullanılan dosya türlerinden olan MS Excel (.xls / .xlsx) ve SPSS (.sav) dosya türleri ile yükleme yapılır. Ek olarak bu menü yüklenen dosyadaki değişkenlerin tipinin ve rolünün belirlenmesini sağlayacak olan ‘Değişkenlerin tipini ve rolünü belirleyiniz’ sekmesini içermektedir.

Normallik analizleri
Web tabanlı uygulamanın bu menüsünde ‘Sayısal değişken(ler)’ sekmesi ile normallik açısından analiz etmek istediğimiz değişkenleri seçebiliriz. Yapılacak analizlerin Tip-I hata düzeyi gerektiğini belirleyen bir ‘anlamlılık düzeyi’ sekmesi vardır. Bu sekme ile analizler 0,01-0,05-0,10 anlamlılık düzeylerinde yapılabilmektedir. Son olarak “Alt grup analizi” sekmesi işaretlenerek gruplar açısından da normallik analizlerini yapmak mümkün olacaktır. Şekil 1, “Normallik Analizleri” menüsünü göstermektedir.

Şekil 1: Normallik analizleri menüsü.

Bu menü ile tek değişkenli ve çok değişkenli normallik analizleri yapılabilmektedir. Tek değişkenli normal dağılıma uygunluk Shapiro-Wilk ve Anderson-Darling testleri ile test edilirken, çok değişkenli normal dağılıma uygunluk ise Mardia’nın çarpıklık-basıklık, Henze-Zirkler ve Doornik-Hansen testleri ile test edilmektedir. Ayrıca testlere ek olarak araştırmacıların kullanımı amacıyla grafiksel metotlardan olan Q-Q, çekirdek yoğunluk kestirim ve 3-boyutlu yüzey grafikleri de yazılımda sonuç çıktıları arasında yer almaktadır.

Geliştirilmiş interaktif web uygulamasının erişilebilirliği ve alıntılanması
Geliştirilen web tabanlı yazılıma
http://biostatapps.inonu.edu.tr/NDY/ adresinden ücretsiz olarak erişilebilir. Bilimsel çalışmalarda yazılımın kaynak gösterilmesi “Arslan, A. K. , Tunc, Z. & Colak, C. Normal Dağılım İnceleme Yazılımı [Web-tabanlı yazılım]” şeklinde yapılabilir. Bu yazılımın geliştirilmesinde shiny ^20, shinyBS ²¹ ve shinythemes ²² paketleri kullanıldı.

Deneysel bulgular
Yazılımın çalışma şeklini gösterebilmek ve çıktılarını inceleyebilmek için iki değişkenden oluşan her bir değişkenin standart normal dağılıma sahip olduğu ve değişkenlerin 1000 gözlem içerdiği veri seti üzerinde normal dağılıma uygunluk analizi gerçekleştirilmiştir. İlk olarak veri seti yazılıma yüklenmiştir. Şekil 2 yüklenen dosyaya ilişkin görüntüleri göstermektedir.

Şekil 2: Yüklenen dosyaya ilişkin görüntüler.

Sonra “Normallik Analizleri” sekmesi ile normalliği kontrol edilmek istenen değişkenler “sayısal değişkenler” sekmesi ile seçilir. Anlamlılık düzeyi belirlenerek normallik analizi yapılır. Şekil 3 Tek değişkenli normal dağılım sonuçlarına ait çıktıları göstermektedir.

Şekil 3: Tek değişkenli normal dağılım sonuçlarına ait çıktılar.

Bu sonuçlara göre iki değişkenden oluşan veri setindeki her bir değişken ayrı ayrı yazılımda normal dağılım göstermektedir. Şekil 4 ise çok değişkenli normal dağılım’ a ait sonuç çıktılarını göstermektedir.

Şekil 4: Çok değişkenli normal dağılım’ a ait sonuç çıktıları.

Bu sonuçlara göre 2 değişkenden oluşan veri seti yazılımda yer alan üç çoklu normal dağılım yöntemine göre de normal dağılmaktadır.

Tek değişkenli veriler için normallik varsayımını kontrol etme genel bir uygulama olarak düşünülürken, çok değişkenli veriler için çok sayıda test olduğu halde normallik varsayımını kontrol etme genelde uygulanmamaktadır ¹⁹. Fakat normallik koşulu sağlanmadan kullanılacak istatistiksel yöntemlerle elde edilen sonuçlar gerçek durumu yansıtmayabilir. Bu yüzden araştırıcılar verilerini analiz etmeden önce mutlaka normallik varsayımı sağlayıp sağlamadığını kontrol etmesi gerekir. Eğer veriler normal dağılıma uygunluk göstermiyorsa uygun dönüşümlerle normallik varsayımı sağlanmaya çalışılır veya parametrik olmayan yöntemler kullanılabilir ²⁴.

Bu çalışmanın amacı araştırıcıların çok değişkenli normal dağılıma uygunluğu kolay bir şekilde kontrol ederek çalışmalarında daha doğru sonuçlar elde etmesini sağlayacak yeni kullanıcı dostu bir web tabanlı yazılım geliştirmektir. Yazılımda çok değişkenli normalliği test etmek için 3 ayrı testten yararlanılmıştır.

Bu testler Mardia’nın çarpıklık-basıklık, Henze-Zirkler ve Doornik-Hansen testleridir. Normalliğe dair sonuç çıktıları araştırıcıların kolayca anlayabileceği şekilde grafiklerle desteklenerek verilmektedir.

İstatistiksel analizler için yaygınca kullanılan IBM SPSS Statistics ^25, Minitab ^26, MedCalc ²⁷ gibi yazılımlarda çoklu normal dağılım yapılmasına imkan sağlayan bir modül bulunmamaktadır. Bu yazılımlara ek olarak Stata ²⁸ programı çoklu normal dağılıma uygunluğu test edebilmektedir. Ancak açık kaynak web tabanlı bir yazılımda tek ve çok değişkenli normal dağılıma uygunluğu değerlendiren az sayıda yazılım vardır. Bunlardan biri Türkiye’de geliştirilen ve MVN: a web-tool for assessing multivariate normality (ver. 1.6) adı verilen yazılımdır ²⁹.

Ayrıca bu çalışmada geliştirilen yazılımın çıktılarını değerlendirebilmek adına iki değişkenli her bir değişkenin standart normal dağılıma sahip olduğu ve 1000 gözlemli veri seti, IBM SPSS Statistics sürüm 25.0 ile türetilmiştir ²⁵. Analiz sonuçlarına göre 2 değişkenin her biri tek değişkenli normal dağılıma uygunluk gösterdi. Ayrıca veri seti çok değişkenli normal dağılımı belirlemek için yazılımda yer verilen üç teste göre de çoklu normal dağılıma uygun olduğu gösterilmiştir.

Sonuç olarak, geliştirilen yazılım tek değişkenli ve çok değişkenli normal dağılıma uygunluk analizlerini kolayca yapabilen ve kullanıcıların yapacakları çalışmalarında daha doğru sonuçlar elde etmesini sağlayan yeni kullanıcı dostu bir web tabanlı yazılımdır. İlerleyen çalışmalarda, en iyi yönteme karar vermede kullanılan ölçütlerden Tip I ve Tip II hata türlerinin yazılıma eklenmesi planlanmaktadır.

1) Peng G. Testing normality of data using SAS. Indianapolis: Lilly Corporate Center, 2004.

2) Pituch KA, Stevens JP. Applied multivariate statistics for the social sciences: Analyses with SAS and IBM’s SPSS: Routledge. 2015.

3) Sharma S, Sharma S. Applied multivariate techniques. 1996.

4) Thode HC. Testing for normality. CRC press, 2002.

5) Mertler CA, Reinhart RV. Advanced and multivariate statistical methods: Practical application and interpretation: Routledge. 2016.

6) Mardia KV. Applications of some measures of multivariate skewness and kurtosis in testing normality and robustness studies. Sankhyā: The Indian J Statist, Series B 1974; 36: 115-28.

7) Gnanadesikan R. Methods for statistical data analysis of multivariate observations. John Wiley & Sons 2011.

8) Darling DA. The kolmogorov-smirnov, cramervon mises tests. The Ann Math Statist 1957; 28: 823-38.

9) Koziol JA. Assessing multivariate normality: a compendium. Commun Stat-Theor M 1986; 15: 2763-83.

10) Mudholkar GS, Srivastava DK, Thomas Lin C. Some p-variate adaptations of the Shapiro-Wilk test of normality. Commun Stat-Theor M 1995; 24: 953-85.

11) Paulson A, Roohan P, Sullo P. Some empirical distribution function tests for multivariate normality. J Stat Comput Simul 1987; 28: 15-30.

12) Ergun M, Çilingir F. İlköğretim bölümünde yapılan lisansüstü tezlerin incelenmesi: Ondokuz Mayıs Üniversitesi örneği. VI Ulusal Lisansüstü Eğitim Sempozyumu 2013; 85.

13) Shapiro SS, Wilk MB. An analysis of variance test for normality (complete samples). Biometrika 1965; 52: 591-611.

14) Özdamar K. Paket Programlar ile istatistiksel veri analizi. Eskişehir: Kaan Kitabevi, 2004.

15) Mardia K. Assessment of multinormality and the robustness of Hotelling's T 2 test. Applied Statistics 1975: 163-71.

16) Mardia KV. Measures of multivariate skewness and kurtosis with applications. Biometrika 1970; 57: 519-30.

17) Henze N, Zirkler B. A class of invariant consistent tests for multivariate normality. Commun Stat-Theor M 1990: 3595-617.

18) Doornik J, Hansen H. Am Omnibus test of univariate and multivariate normality. Oxford: Unpublished paper Nuffield College 1994.

19) Naczk K. Assessing tests for multivariate normality. Carleton University 2005.

20) Cheng J, Xie Y, McPherson J. shiny: web application framework for R. R package version 0.13. 2. 2016.

21) Bailey E. shinyBS: Twitter bootstrap components for shiny. R package version 061 URL https://CRAN R-project org/package= shinyBS 2015.

22) Chang W. shinythemes: Themes for Shiny. R package version 2015; 1:144.

23) Looney SW. How to use tests for univariate normality to assess multivariate normality. ASA 1995; 49: 64-70.

24) Akçadağ Hİ. Tek değişkenli ve çok değişkenli bazı normallik testlerinin karşılaştırılması [Doktora Tezi]. Selçuk Üniversitesi Fen Bilimleri Enstitüsü 2013.

25) Corp I. IBM SPSS statistics for windows, version 22.0. Armonk, NY: IBM Corp 2013.

26) Minitab I. MINITAB statistical software. Minitab Release 2000; 13.

27) Schoonjans F, Zalata A, Depuydt C, Comhaire F. MedCalc: a new computer program for medical statistics. Comput Methods Programs Biomed 1995; 48: 257-62.

28) StataCorp L. Stata data analysis and statistical Software. Special Edition Release 2007; 10: 733.

29) Korkmaz S, Goksuluk D, Zararsiz G. MVN: An R package for assessing multivariate normality. RJ 2014; 6: 151-62.